Budowa atomu

Odkrycie ciał promieniotwórczych przyczyniło się w dużym stopniu do poznania budowy atomów. Naturalne ciała promieniotwórcze wysyłają promienie α, β i γ. Promienie α są strumieniem podwójnie zjonizowanych atomów helu niosących po dwa elementarne ładunki dodatnie. Promienie β są strumieniem swobodnych elektronów wyrzucanych z jądra, a γ stanowią strumień promieniowania elektromagnetycznego o długości fali rzędu 10^-13 m. Zgodnie ze wzorem na siłę Lorentza w polu magnetycznym cząstki α i β ulegają odchyleniu w przeciwnych kierunkach, a promienie γ nie doznają odchylenia.

(Rys. 2.1)

Po uzyskaniu w rurze do wyładowań lecących elektronów (promienie katodowe) oraz protonów czy innych cząstek dodatnio naładowanych (promienie kanalikowe) jasnym się stało, że materia zawiera oba te składniki. Thomson wysunął w 1897 roku hipotezę, że składniki te są rozmieszczone równomiernie wewnątrz atomu, a w roku 1911, w związku z doświadczeniami nad rozpraszaniem cząstek α (Geiger, Marsden, 1908) na cienkich foliach złota i innych metali, Rutherford zaproponował nowy model budowy atomu. Badając rozproszenie cząstek α uczniowie Rutherforda: Geiger i Marsden stwierdzili, że większość tych cząstek przechodzi przez folie bez odchylenia, a tylko niektóre z nich zostają odchylone pod dużymi kątami, a nawet odrzucone wstecz. Fakt, że większość cząstek α przechodzi przez folię złota bez odchylenia świadczy o tym, że dla większości cząstek folia stanowi pustą przestrzeń. Z drugiej strony było wiadomo, że cząstki α muszą napotykać na swojej drodze silne pole kulombowskie występujące wewnątrz atomu i że rozproszenie cząstki α pod dużym kątem zachodzi wskutek działania jednego atomu folii. Dla wytłumaczenia istnienia tak silnego pola, Rutherford założył, że cały ładunek dodatni Ze⁺ atomu jest skupiony w bardzo małym jądrze, które zawiera również prawie całą masę atomu. Elektrony zajmują pozostałą przestrzeń atomu i są rozmieszczone dookoła jądra. Z powodu małej masy elektronów Rutherford zaniedbał oddziaływanie elektronów na cząstki α.

Rozwijając teorię rozpraszania cząstek α Rutherford założył dalej, że cząstki α oraz jądro stanowią ładunki punktowe oraz że prawo Coulomba i prawa mechaniki newtonowskiej są słuszne również dla małych odległości. Zgodnie z tymi założeniami między cząstką α a jądrem działa siła odpychania

(2.1)

gdzie r oznacza odległość cząstki α od jądra atomu folii. Z praw mechaniki wynika, że pod wpływem tego rodzaju siły cząstka porusza się po krzywej stożkowej. W przypadku siły przyciągającej, np. siły grawitacji między Słońcem a planetami, orbitami są parabole i elipsy, a w przypadku szczególnym okręgi lub linie proste. Jeżeli siły są odpychające orbitą jest gałąź hiperboli lub, w przypadku szczególnym, linia prosta. Siła odpychająca działa równocześnie na cząstkę α i na jądro atomu, ponieważ jednak jądro złota (Z = 79) ma masę wiele razy większą od masy cząstki α więc można przyjąć, że jądro pozostaje w spoczynku. Jeżeli cząstka α porusza się dokładnie w kierunku jądra, to siła hamująca będzie narastać w miarę zbliżania się cząstki α do jądra, aż do chwili jej zatrzymania, po czym rozpocznie się odpychanie, czyli ruch przyspieszony cząstki α w kierunku przeciwnym, wzdłuż tej samej prostej, po której cząstka zbliżała się do jądra, przy czym cały ruch cząstki α odbywa się po linii prostej. W przypadku rozproszenia wstecznego następuje zmiana kierunku toru o 180°. Jest to przypadek bardzo rzadki gdyż, wówczas cząstka α musiałaby się poruszać wzdłuż prostej przechodzącej przez jądro, którego rozmiary są bardzo małe.

W momencie zatrzymania się cząstki α jej energia kinetyczna zamienia się na energię potencjalną pola kulombowskiego jądra, przy czym

(2.2)

gdzie: M – masa cząstki, v – jej prędkość, d – minimalna odległość na jaką cząstka α może się zbliżyć do jądra wskutek istnienia odpychających sił kulombowskich. Promień jądra nie może być zatem większy od tej wielkości.

Częściej jednak zachodzi przypadek, gdy pierwotny tor ruchu cząstki α przechodzi w pewnej odległości od jądra. Załóżmy, że jądro o ładunku Ze znajduje się w punkcie C, a cząstka α o ładunku 2e i masie M zbliża się do jądra wzdłuż prostej AB z prędkością v (Rys. 2.2)

(Rys. 2.2)

Pod wpływem siły odpychającej cząstka α zostaje odchylona od pierwotnego kierunku o kąt θ i porusza się po hiperboli, przy czym jądro atomu znajduje się w jej ognisku po stronie wypukłej. Proste AB i OD są asymptotami hiperboli – wzdłuż nich porusza się cząstka α, gdy znajduje się w dużej odległości od jądra.

Kąt θ jest zależny od tzw. parametru zderzenia p zgodnie ze wzorem, który podajemy bez dowodu

(2.3)

Parametr zderzenia p jest to odleglośc jądra od pierwotnego kierunku lotu cząstki α. Przyjmując oznaczenie

(2.4)

mamy

(2.5)

Niech n oznacza liczbę atomów w 1 cm³ materiału folii, t zaś grubośc folii; wówczas na jednostkę powierzchni folii przypada nt atomów. Cząstka α przechodząc w odległości p od jądra zostaje odchylona pod kątem θ (albo pod kątem większym od kąta θ) który jest określony wzorem (2.3). W celu wyznaczenia prawdopodobieństwa, że cząstka α będzie przechodzić w odległości p od jądra, wyobraźmy sobie koła o promieniu p zatoczone wokół każdego jądra. Powierzchnia, jaką zajmują wszystkie te koła, wynosi πp²nt. Prawdopodobieństwo f, że cząstka α przejdzie w odległości p (lub mniejszej) od jądra (lub innymi słowy będzie rozproszona pod kątem równym lub większym od θ) jest równe sumarycznej powierzchni przekroju πp²nt wszystkich jąder znajdujących się wewnątrz warstwy o jednostkowej powierzchni przekroju, czyli

(2.6)

Na przykładzie rozpraszania cząstek α omówimy pewne pojęcia, z którymi często spotykamy się w fizyce współczesnej, mianowicie całkowity przekrój czynny i różniczkowy przekrój czynny.

Wprowadzając oznaczenia σ = πp², możemy napisać, że prawdopodobieństwo f rozproszenia cząstki α pod kątem θ lub większym od θ wynosi

(2.7)

Jeżeli na folię pada Q cząstek, to liczba cząstek rozproszonych N będzie wynosić

(2.8)

i stąd przekrój czynny σ jest określony równością

(2.9)

Jest to definicja całkowitego przekroju czynnego, wynikająca z doświadczenia (pomiarów). Jednostką przekroju czynnego jest 1 barn = 10^-24 cm². We wzorze (2.7) przekrój czynny σ jest miarą prawdopodobieństwa zajścia danego procesu (rozproszenia pod kątem θ lub pod kątem większym od θ).

Różniczkując związek

(2.10)

otrzymujemy

(2.11)

czyli

(2.12)

Wielkość dσ nazywamy różniczkowym przekrojem czynnym; jest ona miarą prawdopodobieństwa, że cząstka α zostanie rozproszona pod kątem zawartym w przedziale (θ,θ+dθ). Cząstki α rozproszone pod kątem zawartym między θ i θ+dθ poruszają się w przestrzeni ograniczonej bocznymi powierzchniami stożków współosiowych o półkątach rozwarcia przy wierzchołkach θ i θ+dθ.

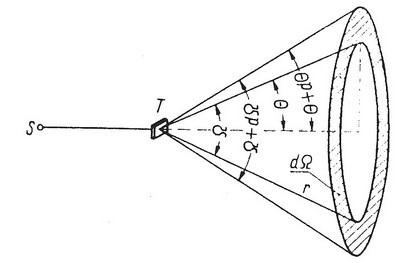
Jeżeli wyobrazimy sobie ekran ustawiony każdorazowo prostopadle do kierunku lotu cząstek α rozproszonych w przedziale (θ,θ+dθ), to powierzchnia bombardowana przez te cząstki będzie miała kształt pierścienia o szerokości rdθ, wyciętego z powierzchni kuli o promieniu r, zatoczonej wokół jądra rozpraszającego (Rys. 2.3).

(Rys. 2.3)

Promień tego pierścienia wynosi rsinθ, a jego powierzchnia

(2.13)

Stosunek

(2.14)

określa element kąta przestrzennego, do którego rozpraszane są cząstki α. Zatem

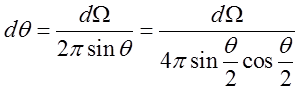(2.15)

czyli

(2.16)

W doświadczeniach Geigera i Marsdena wyznaczono liczbę cząstek α rozproszonych pod kątem zawartym w przedziale (θ,θ+dθ) i padających na jednostkową powierzchnię przez liczenie scyntylacji (błysków świetlnych), które powstają w miejscu uderzenia pojedynczych cząstek α w ekran fluoryzujący, np. z siarczku cynku. Jeżeli przez Q oznaczymy całkowitą liczbę cząstek wysyłanych przez źródło, to liczba dN cząstek rozproszonych, padających na jednostkę powierzchni ekranu znajdującego się w odległości r od folii, wynosi

(2.17)

Ze wzoru tego wynika, że liczba cząstek rozproszonych pod kątem θ jest:

a) proporcjonalna do grubości t folii

b) odwrotnie proporcjonalna do kwadratu energii kinetycznej cząstek α

c) odwrotnie proporcjonalna do sin⁴θ/2

d) odwrotnie proporcjonalna do kwadratu odległości ekranu od folii.

Doświadczenia Geigera i Marsdena wykonane dla folii ze złota, srebra, miedzi i aluminium potwierdziły słuszność teorii Rutherforda, na ich podstawie jednak nie można było bezbłędnie wyznaczyć liczby porządkowej atomu Z.

Na rysunku 2.4 jest przedstawiony schemat aparatury Rutherforda do badania rozpraszania cząstek α. Puszka B w kształcie walca jest przymocowana do koła A zaopatrzonego w podziałkę i można ją razem z kołem A obracać dzięki zaopatrzeniu podstawy A w szlif C. Preparat radioaktywny R oraz folia rozpraszająca F są przymocowane do osobnej rurki T, niezależnej od puszki B w celu utrzymania stałego położenia preparatu R względem folii F przy dowolnym ustawieniu puszki B oraz mikroskopu M. Do obiektywu mikroskopu jest przymocowany przezroczysty ekran fluoryzujący S.

(Rys. 2.4)

2.1.1 Doświadczenie Chadwicka

Dopiero Chadwickowi w roku 1923 udało się dokładnie wyznaczyć ładunek jądra Ze. W doświadczeniu Chadwicka cząstki α wychodzące ze źródła R trafiają na folię metalu w postaci pierścienia A i po rozproszeniu są rejestrowane na ekranie S (Rys. 2.5).

(Rys. 2.5)

Między źródłem R a ekranem S znajduje się tarcza ołowiana B, która nie przepuszcza cząstek lecących w linii prostej ze źródła do ekranu. Z porównania rys 2.3 i 2.5 widać, że u Chadwicka powierzchnia folii rozpraszającej, z której są rejestrowane odchylone cząstki α, jest większa niż w doświadczeniu Geigera Marsdena.

Doświadczenie Chadwicka jest jedynym, umożliwiającym bezpośredni pomiar ładunku jądra. Otrzymane rezultaty potwierdziły zgodność doświadczenia z teorią Rutherforda o budowie jądra atomowego.

2.2 Budowa atomu

Zgodnie z hipotezą Rutherforda atom każdego pierwiastka jest zbudowany z jądra i powłok elektronowych. Fakt, że masy wszystkich izotopów danego pierwiastka wyrażają się liczbą zbliżoną do całkowitej, nasówał wniosek, że jądra atomów zbudowane są z cząstek, tzw. nukleonów, o względnej masie atomowej zbliżonej do jedności. Znane są dwie cząstki – proton i neutron, których masy różnią się nieznacznie od jedności. Proton i neutron uważa się obecnie za dwa różne stany ładunkowe tej samej cząstki – nukleonu. Hipoteza, że jądro jest zbudowane z neutronów i protonów została wysunięta w roku 1932 przez Heisenberga i Iwanienkę po odkryciu w tymże roku przez Chadwicka neutronów.

Rozmiary atomu są rzędu 10^-10 m, a rozmiary jądra 10^-15 m. Okazuje się, że objętość jądra jest proporcjonalna do liczby nukleonów w jądrze, czyli

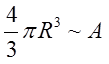(2.18)

wówczas promień R jądra dowolnego pierwiastka o liczbie nukleonów A wyrazi się wzorem

(2.19)

gdzie R₀ = 1,2 ⋅ 10^-15 m jest promieniem jądra wodoru. Tak np. dla atomu argonu, dla którego A = 40, promień jądra R = 4,4 ⋅ 10^-15 m, gdy promień atomu tego pierwiastka wynosi 1,5 ⋅ 10 ^-10 m, czyli jest około 4 ⋅ 10⁴ razy większy. Powierzchnia rzutu jąder wszystkich atomów folii o grubości 0,025 mm na płaszczyznę równoległą do folii stanowi zaledwie 1/10⁴ część całkowitej powierzchni folii. Gęstość substancji jądrowej jest stałą dla wszystkich jąder i wynosi

(2.20)

Jednostką masy atomowej (j.m.a.) jest masa 1/12 masy izotpou węgla ¹²C, przy czym

(2.21)

Korzystając z relacji Einsteina E = mc² otrzymujemy

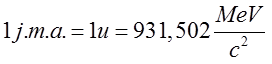(2.22)

W atomowych jednostkach masy masy protonu i neutronu wynoszą odpowiednio:

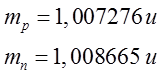(2.23)

Dla pierwiastków lekkich liczba protonów Z w jądrze jest równa liczbie neutronów N czyli N/Z ≈ 1. Dla jąder pierwiastków, znajdujących się na końcu układu okresowego, stosunek N/Z ≈ 1,6. Liczba Z zwana liczbą atomową albo liczbą porządkową i określa łądunek dodatni jądra Ze⁺ oraz liczbę elektronów w atomie. Liczba nukleonów A = N + Z w jądrze nazywa się liczbą masową i określa w przybliżeniu masę danego pierwiastka.

2.3 Serie widmowe atomu wodoru

Jedną z podstawowych dróg poznania struktury atomów dowolnego pierwiastka jest badanie wysyłanego albo absorbowanego przez atomy promieniowania. Pierwiastki w postaci gazu lub pary wysyłają promieniowanie o charakterystycznym dla danego pierwiastka widmie złożonym z ostrych linii. Widma te są badane przy użyciu spektrometrów lub spektroskopów. Widma atomów są w większości bardzo złożone, tak że wyznaczanie długości fal oraz natężeń poszczególnych linii widmowych jest trudne.

W wyniku żmudnych badań stwierdzono, że linie widmowe danego pierwiastka można opisać prostymi równaniami i że są zgrupowane w tak zwane serie, przy czym linie widmowe jednej serii mogą zachodzić na inną serię. Prawa serii widmowych pierwiastków wskazują wyraźnie na istnienie dyskretnych stanów energetycznych atomów, o czym będzie mowa dalej.

Najprostszą budowę ma atom wodoru, co odzwierciedla się również w prostocie jego widma. Z tych też względów atom wodoru jest najdokładniej zbadany zarówno teoretycznie jak i doświadczalnie, gdyż zachodzące tu prawidłowości najłatwiej stwierdzić.

W widmie atomu wodoru zaobserwowano następujące serie:

Lymana (ultrafiolet):

(2.24)

Balmera (widzialna):

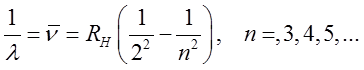(2.25)

Paschena (podczerwień):

(2.26)

Bracketta:

(2.27)

Pfunda:

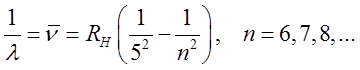(2.28)

Humphreysa:

(2.29)

Zapis serii widmowej w podobnej postaci był podany po raz pierwszy przez Balmera (1885) dla serii widmowej wodoru nazwanej jego imieniem. We wzorach powyższych R_H oznacza stałą Rydberga dla wodoru, przy czym

(2.30)

a odwrotność długości fali

(2.31)

jest tzw. liczbą falową. Ponieważ

(2.32)

i serie widmowe wodoru można zapisać ogólnym wzorem

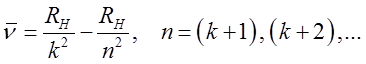(2.33)

gdzie k jest liczbą całkowitą, inną dla każdej serii, lub też w prostszej postaci

(2.34)

Liczby T_k i T_n nazywamy termami

2.4 Teoria Bohra budowy atomu wodoru

Empiryczny wzór Balmera został wyprowadzony teoretycznie po raz pierwszy przez duńskiego fizyka Nielsa Bohra (1913). Podana przez Bohra teoria budowy atomu wodoru, która odegrała bardzo istotną rolę w rozwoju mechaniki kwantowej, została z biegiem czasu zmodyfikowana i dziś ma już znaczenie historyczne. Bohr przyjął za podstawę swego rozumowania teorię Rutherforda budowy atomu, według której atom wodoru zawiera proton jako jądro oraz jeden elektron krążący wokół jądra. Między tymi cząstkami działa kulombowska siła centralna

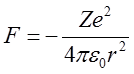(2.35)

pod wpływem której elektron porusza się wokół jądra po krzywej stożkowej.

W przypadku wodoru (Z = 1) z dobrym przybliżeniem można przyjąć, że torem elektronu jest okrąg o promieniu r. Dla ruchu elektronu po okręgu zachodzi związek

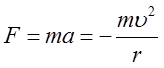(2.36)

gdzie m jest masą elektronu. Znak minus w obu wzorach oznacza, że siła jest skierowana do środka okręgu. Przyrównując obie siły otrzymujemy

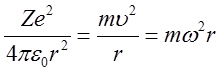(2.37)

A więc energia kinetyczna elektronu

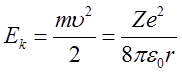(2.38)

Jądro o ładunku Ze wytwarza pole, które w odległości r ma potencjał

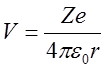(2.39)

Wobec tego elektron umieszczony w odległości r od jądra ma energię potencjalną

(2.40)

Całkowita energia E elektronu wynosi zatem

(2.41)

Jako poziom odniesienia dla energii potencjalnej atomu przyjmuje się U = 0 dla r = ∞. Gdy więc elektron znajduje się w nieskończoności, atom wodoru ma maksymalną energię, równą zeru. Dla każdego innego położenia elektronu energia atomu wodoru jest mniejsza (ujemna).

Zastanówmy się jeszcze nad klasycznym obrazem budowy atomu wodoru. Według elektrodynamiki klasycznej atom wodoru powinien wypromieniowywać energię i to proporcjonalnie do kwadratu przyspieszenia elektronu. Częstotliwość promieniowania powinna być taka sama jak mechaniczna częstotliwość

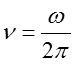(2.42)

ruchu elektronu dookoła jądra. Ponieważ

(2.43)

W miarę jak atom promieniowałby, jego energia malałaby, a to pociągałoby za sobą zmniejszanie się promienia orbity elektronu, czyli wzrost częstotliwości mechanicznej ruchu i wzrost częstotliwości energii wypromieniowywanej. W rezultacie widmo promieniowania wysyłanego przez atom powinno być ciągłe o rosnącej częstotliwości, a elektron powinien wpaść do jądra.

Doświadczenie nie potwierdza tego obrazu klasycznego. Aby wytłumaczyć istnienie wyraźnych serii, jakie występują w widmie atomu wodoru, Bohr wprowadził następujące postulaty:

1) Elektron nie może krążyć po dowolnej orbicie, lecz tylko po tych, dla których moment pędu (kręt) elektronu jest wielokrotnością h/2π. Każdej orbicie odpowiada inny stan energetyczny atomu. Znajdując się na orbicie dozwolonej elektron nie promieniuje energii. Orbity dozwolone zostały nazwane stacjonarnymi. Zakładając, że ruch elektronu odbywa się po orbicie kołowej, pierwszy postulat Bohra można zapisać następująco

(2.44)

gdzie n jest liczbą całkowitą.

2) Drugi postulat Bohra mówi, że atom absorbuje lub emituje promieniowanie w postaci kwantu o energii hν przechodząc z jednego stanu energetycznego E_n do drugiego E_k (czyli przy przejściu elektronu z jednej orbity dozwolonej na inną). Różnica energii tych stanów atomu równa się energii wypromieniowanego kwantu

(2.45)

We wzorze tym E_n oznacza energię atomu w stanie początkowym, E_k – w stanie końcowym, ν – jest częstotliwością emitowanego lub zaabsorbowanego promieniowania. Energia zostaje wypromieniowana, gdy E_n > E_k, pochłonięta zaś jeżeli E_n < E_k. Po podniesieniu równania 2.44 do kwadratu

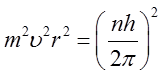(2.46)

i przekształceniu równania 2.37

(2.47)

a następnie podzieleniu pierwszego równania przez drugie, otrzymujemy

(2.48)

Wielkości występujące w tym wzorze były już omówione wcześniej. Wstawiając do wzoru 2.48 ich wartości liczbowe otrzymujemy na r dla n = 1 wartość liczbową

(2.49)

Promień pierwszej orbity elektronu a₀ jest równy promieniowi atomu wodoru. Warto tu zwrócić uwagę na to, że teoria kinetyczna gazów przewiduje na rozmiary atomu wartości dobrze zgadzające się z wartościami obliczonymi z teorii Bohra.

Promienie dalszych orbit wzrastają jak kwadraty n, tzn.

(2.50)

Energię elektronu znajdującego się w atomie na n – tej orbicie otrzymujemy wstawiając do wzoru (2.41) wartość r ze wzoru (2.48)

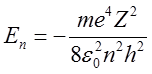(2.51)

Częstotliwość promieniowania emitowanego przez atom przy przejściu elektronu z orbity n na orbitę k wynosi

(2.52)

a liczba falowa

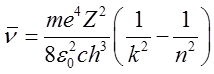(2.53)

Wzór ten ma kształt podobny do wzorów na serie widmowe przy założeniu, że wyraz

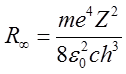(2.54)

oznacza stałą Rydberga. Wstawiając do wzoru (2.54) na R_∞ wartości otrzymane na m, e, c, h z niezależnych eksperymentów oraz Z = 1, otrzymujemy wartość stałej R_∞ dla wodoru przewidywaną przez teorię Bohra

(2.55)

która dobrze zgadza się z wartością stałej Rydberga dla wodoru otrzymaną z pomiarów spektroskopowych

(2.56)

Ta zgodność przewidywań teorii Bohra z doświadczeniem była silnym bodźcem do dalszego rozwoju mechaniki kwantowej, zapoczątkowanej teorią Bohra i teorią Plancka.

Każdy atom może emitować w danej chwili tylko jeden foton. Dana ilość wodoru zawiera olbrzymią ilość atomów, z których każdy może emitować jeden foton, lecz o różnej częstotliwości, przez co powstaje całe widmo wodoru, które obserwujemy doświadczalnie. Liczba atomów emitujących poszczególne linie widmowe określa natężenie tych linii.

Na rysunku (2.6) są przedstawione przejścia kwantowe elektronów wewnątrz atomu wodoru zapoczątkowujące poszczególne serie widmowe wodoru, a na rysunku (2.7) położenia linii poszczególnych serii widmowych wodoru.

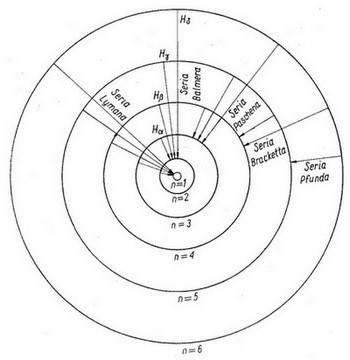(Rys. 2.6)

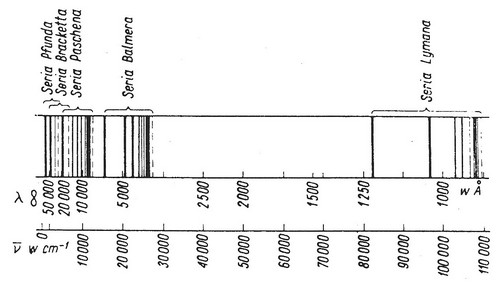(Rys. 2.7)

Porównanie wzoru

(2.57)

ze wzorem

(2.58)

wskazuje na to, że liczba falowa każdej linii widmowej jest różnicą dwóch termów, przy czym pierwszy wyraz (ze znakiem minus) z wzoru ostatniego przedstawia energię stanu końcowego podzieloną przez ch, drugi zaś energię stanu początkowego podzieloną przez ch.

(2.59)

Diagram poziomów energetycznych atomu wodoru bez uwzględnienia struktury subtelnej, o której będzie mowa niżej przedstawia rysunek (2.8). Poziomy energetyczne są na nim narysowane jako linie poziome. Na rysunku tym pokazano również skalę liczb falowych w cm^-1. Najniższy stan energetyczny jest stanem podstawowym wodoru. Przejście z dowolnego stanu do stanu podstawowego daje linie serii Lymanna. Przejście z dowolnego stanu (n) do najniższego stanu wzbudzonego (k = 2) daje serię Balmera.

(Rys. 2.8)

2.5 Wpływ ruchu jądra na wartość stałej Rydberga. Masa zredukowana elektronu

Bohr założył początkowo, że jądro atomu jest w spoczynku, a wokół niego krąży elektron. Założenie to byłoby spełnione, gdyby masa jądra była nieskończenie duża w porównaniu z masą elektronu. Ponieważ tak nie jest, więc w rzeczywistości elektron i jądro krążą wokół wspólnego środka masy. Oznaczając masę jądra przez M, odległość elektronu i jądra od środka obrotu odpowiednio przez a i A, otrzymujemy związki

(2.60)

Stąd

(2.61)

Oznaczając prędkości liniowe elektronu i jądra odpowiednio przez v i V mamy

(2.62)

gdzie ω jest wspólną prędkością kątową obiegu elektronu i jądra.

Sumaryczna energia kinetyczna elektronu i jądra

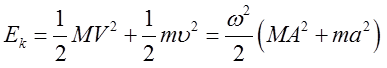(2.63)

wstawiając na miejsce a i A poprzednio wyznaczone związki otrzymujemy ostatecznie

(2.64)

gdzie

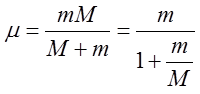(2.65)

Wyraz μ nazywamy masą zredukowaną elektronu, przy czym μ < m

(2.66)

Sumaryczny moment pędu (kręt) jądra i elektronu wynosi

(2.67)

Zgodnie z postulatem Bohra, sumaryczny moment pędu wynosi nh/2π, czyli

(2.68)

W analogii do wzoru (2.48) otrzymujemy

(2.69)

Wstawiając tę wartość do wzoru (2.41) na energię całkowitą mamy

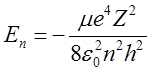(2.70)

Korzystając z drugiego postulatu Bohra znajdujemy liczbę falową dla atomu wodoru (Z = 1) w postaci

(2.71)

gdzie

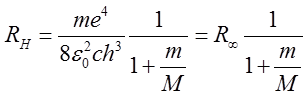(2.72)

przy czym R_∞ jest stałą Rydberga dla atomu wodoru (Z = 1) przy założeniu, że jądro jest nieruchome

(2.73)

Dla atomów o liczbie porządkowej Z, zjonizowanych tak, że mają tylko jeden elektron otrzymujemy serie widmowe analogiczne do serii widmowych wodoru z tym, że we wzorze (2.72) wyraz e⁴ należy zmienić na Z²e ⁴ (kwadrat ładunku jądra razy kwadrat ładunku elektronu). Zatem dla takiego atomu liczbę falową wyraża wzór

(2.74)

gdzie M jest masą danego jądra, m – masą elektronu. Stała Rydberga

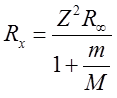(2.75)

dla pierwiastka zjonizowanego (wodoropodobnego) zależy od masy atomowej M tego pierwiastka. Znajomość stałej Rydberga R_x i porównanie ją ze stałą Rydberga R_H dla wodoru, może posłużyć do wyznaczenia stosunku M_H/m; np. mamy

(2.76)

i korzystając ze związku

(2.77)

otrzymujemy

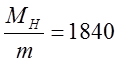(2.78)

co jest w dobrej zgodności z wartością otrzymaną z innych doświadczeń.

2.6 Odkrycie deuteru

Zależność stałej Rydberga R_x oraz częstotliwości linii widmowych od masy jądra przyczyniły się do wykrycia deuteru to jest ciężkiego izotopu wodoru o liczbie masowej A = 2. Mianowicie porównując wyniki dokładnych pomiarów masy atomu wodoru, przeprowadzone przez Astona spektrografem masowym, z wynikami pomiarów chemicznych Borge i Menzel stwierdzili, że pomiary chemiczne dawały wartość o 0,02% większą. Borge i Menzel (1931) wyrazili przypuszczenie, iż niezgodność ta pochodzi stąd, że wodór naturalny zawiera dwa izotopy wodoru ¹H i ²H w stosunku 4500:1.

W celu wykrycia deuteru Urey, Murphy i Brichwedde (1932) przeprowadzili szereg pomiarów serii Balmera w widmie wodoru przy użyciu spektrografu z wklęsłą metalową siatką dyfrakcyjną o szerokości 54 cm. Otrzymali oni słaby obraz linii, co do której przypuszczali, że jest to linia H_β izotopu ²H. Wyniki te sprawdzili następnie na próbkach wodoru o większej zawartości izotopu ²H, które otrzymali przez odparowywanie ciekłaego wodoru: 1) przy ciśnieniu normalnym, 2) przy ciśnieniu nieco wyższym niż ciśnienie punktu potrójnego. Dla obu tych próbek intensywność linii H_β izotopu ²H, była wzmocniona w stosunku do próbki wodoru zwykłego.

Wkrótce po odkryciu deuteru stwierdzono, że resztki wody po elektrolizie są wzbogacone w ten izotop. Ta metoda umożliwiła otrzymywanie ciężkiej wody i deuteru w większej ilości. Deuter znalazł szersze zastosowanie w badaniach chemicznych, biologicznych i fizycznych. W fizyce jądrowej deuter oraz jego jądra, zwane deuteronami, oddały nieocenione usługi.

2.7 Orbity eliptyczne

Postulat Bohra odnoszący się do kwantowania momentu pędu możemy zapisać w postaci

(2.79)

i wysłowić ogólnie: atomowe wielkości mechaniczne o wymiarach stałej Plancka nie mogą przyjmować wartości dowolnych, lecz są zawsze całkowitą wielokrotnością stałej Plancka. Położenia elektronu w atomie, dla których te wielkości są wielokrotnościami stałej Plancka, odpowiadają stanom stacjonarnym.

Postulat Bohra umożliwia wyróżnienie stacjonarnych orbit kołowych. Z mechaniki klasycznej wiadomo, że pod wpływem sił centralnych (siły kulombowskie) ciało może poruszać się zarówno po orbicie kołowej, jak i eliptycznej. Ruch po okręgu na określonej płaszczyźnie ma tylko jeden stopień swobody, ruch po elipsie na tej samej płaszczyźnie ma dwa stopnie swobody. Dlatego też warunek kwantowania Bohra wystarczający dla wyboru (wyróżnienia) stacjonarnych orbit kołowych nie wystarcza dla wyboru stacjonarnych orbit eliptycznych.

Metoda kwantowa Bohra została poszerzona przez Sommerfelda, który udowodnił, że dla każdego stopnia swobody ruchu należy podać osobny warunek kwantowania. Dla sformułowania tych warunków kwantowania Sommerfeld wykorzystał tzw. współrzędne uogólnione.

Przez współrzędne uogólnione rozumiemy w mechanice wielkości, które jednoznacznie określają położenie punktu, biorącego udział w ruchu o określonej liczbie stopni swobody. Ruch punktu po okręgu można określić we współrzędnych biegunowych przez podanie kąta φ. Ruch punktu po elipsie określa promień wodzący r i kąt φ.

Współrzędne r, φ będziemy nazywać współrzędnymi uogólnionymi q_i. Każdej współrzędnej uogólnionej q_i odpowiada pęd uogólniony p_i, określony następującym związkiem

(2.80)

gdzie E_k jest energią kinetyczną cząstki poruszającej się zaś q_i (z kropką) jest pochodną czasową współrzędnej uogólnionej. Ponieważ energię kinetyczną cząstki można zapisać w postaci

(2.81)

więc

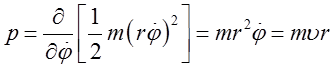(2.82)

Pędem uogólnionym w przypadku ruchu po okręgu jest moment pędu cząstki.

W przypadku ruchu jednostajnego po okręgu moment pędu ciała jest stały

(2.83)

warunek Bohra można więc zapisać następująco

(2.84)

W przypadku ruchu elektronu po elipsie zmianom okresowym ulega zarówno kąt φ jak i promień r. Orbity eliptyczne są zatem określone przez dwa warunki kwantowania

(2.85)

gdzie k nazywa się kątową lub azymutalną liczbą kwantową, zaś n_r – radialną liczbą kwantową.

Można wykazać, że energia całkowita elektronu w ruchu po orbicie zależy jedynie od wielkości dużej półosi a elipsy i wynosi

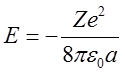(2.86)

Oczywiście dalej słuszny pozostaje wzór (2.51)

(2.87)

Wzór ten jest analogiczny do wzoru na energię dla orbit kołowych. We wzorze tym n oznacza główną liczbę kwantową, przy czym

(2.88)

Korzystając ze wzorów (2.86) i (2.51) dla dużej półosi elipsy otrzymujemy

(2.89)

Przy powyższych oznaczeniach mała półoś

(2.90)

(co podajemy bez dowodu), gdzie

(2.91)

jest promieniem pierwszej orbity Bohra. Duża półoś jest określona główną liczbą kwantową n, zaś mała półoś – główną i azymutalną liczbą kwantową. Ponieważ n = n_r + k, więc dla n = 1 możliwe są dwa warianty: n_r = 1, k = 0 oraz n_r = 0, k = 1. Wartość k = 0 należy wykluczyć z dalszych rozważań, ponieważ dla k = 0 orbita eliptyczna zamienia się w linię prostą, co oznaczałoby, że dla k = 0 elektron oscyluje względem jądra przechodząc przez nie, a to jest nie możliwe ze względu na strukturę jądra.

Najmniejszą spośród możliwych wartości k jest zatem k = 1. Przy wartości n = k = 1 pierwsza orbita eliptyczna jest okręgiem, czyli jest równa pierwszej orbicie Bohra. Dla n = 2, k = 1 albo k = 2, są więc możliwe dwie orbity: elipsa i okrąg. Dla n = 3, k = 1, 2, 3, możliwe są trzy orbity: 2 elipsy i okrąg (Rys. 2.9)

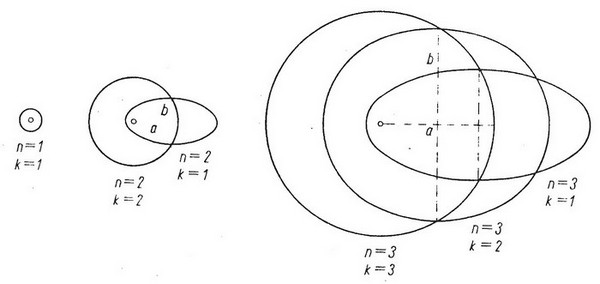(Rys. 2.9)

Wprowadzenie zamiast jednego warunku kwantowania dwóch, nie dało nowych poziomów energetycznych ani nowych linii widmowych. Ten fakt wynika stąd, że współrzędne uogólnione φ i r podlegają zmianom okresowym w tym samym czasie i z tym samym okresem. Z rozważań matematycznych nad układami multiokresowymi wynika, że zawsze gdy stosunek okresów dwóch różnych wielkości układu jest liczbą wymierną, oba warunki kwantowe sprowadzają się (degenerują się) do jednego. Jedynie gdy stosunek okresów jest liczbą niewymierną, warunek kwantowy dla każdej wielkości

(2.92)

ma wpływ na poziomy energetyczne układu. Taki układ nazywamy układem niezdegenerowanym.

2.8 Poprawka relatywistyczna przy obliczaniu poziomów energetycznych

W ruchu po elipsie w różnych miejscach toru elektron ma różną prędkość, co prowadzi do relatywistycznej zmiany jego masy. Sommerfeld wykazał, że relatywistyczna zmiana masy elektronu w ruchu po elipsie powoduje, że tor elektronu jest rozetą (Rys. 2.10).

(Rys. 2.10)

Powstanie tej rozety wynika stąd, że elektron porusza się po orbicie eliptycznej, której duża oś precesuje powoli w płaszczyźnie elipsy wokół osi przechodzącej przez jeden z biegunów elipsy. Ta poprawka relatywistyczna objawia się tym, że we wzorze na energię dochodzi dodatkowy wyraz ΔE, zależny od azymutalnej liczby kwantowej k

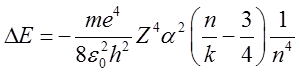(2.93)

gdzie

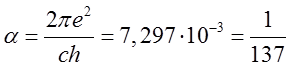(2.94)

nosi nazwę stałej Sommerfelda struktury subtelnej. Zależność poziomu energetycznego od liczby kwantowej k powoduje bowiem, że dany poziom rozszczepia się na n termów leżących bardzo blisko siebie. Dla n = 1 mamy k = 1, występuje zatem tylko jeden poziom energetyczny. Dla n = 2, mamy k = 1 lub k = 2, a więc występują dwa poziomy energetyczne, dla n = 3 – trzy poziomy energetyczne itp. Przy przejściu elektronu z warstwy o głównej liczbie kwantowej n = 3 do warstwy o liczbie n = 2 otrzymujemy linię H_α serii Balmera. Ponieważ dla n = 3 azymutalna liczba kwantowa k może przyjmować wartości 3, 2, 1, a dla n = 2 wartości k = 2 lub 1, mamy zatem 6 możliwych sposobów realizacji przejścia z warstwy n = 3 do warstwy n = 2. Należałoby oczekiwać, że zamiast jednej linii H_α wystąpi aż 6 linii, różniących się nieznacznie częstotliwością ν, czyli wystąpi tzw. struktura subtelna; jeżeli dana linia widmowa rozpada się na kilka linii leżących blisko siebie, powiadamy, że linia ta ma strukturę subtelną. Doświadczenie wykazuje, że zamiast oczekiwanych 6 linii, linia H_α składa się z trzech linii leżących blisko siebie. Jest to spowodowane tym, że Δk, czyli zmiana wartości k jest ograniczona regułami wyboru, mianowicie

(2.95)

2.9 Hipoteza de Broglie’a a kwantowanie orbit

Omówiony poprzednio model atomu Bohra jest modelem poglądowym i z tych względów ułatwia przejście z fizyki klasycznej do mechaniki kwantowej. Jest rzeczą zadziwiającą, że model ten dawał prawie poprawne wyniki dotyczące budowy atomu. Przyczyna tego jest dwojaka:

1) dla wytłumaczenia zjawisk atomowych potrzebowaliśmy jedynie sił elektrycznych, które są dobrze znane w zjawiskach makroskopowych,

2) mimo, że tylko mechanika kwantowa daje poprawne rozwiązanie zagadnień atomowych, dopuszcza ona jednak mechanikę klasyczną jako pierwsze przybliżenie.

Właściwe rozwiązanie zagadnień atomowych i jądrowych można otrzymać jedynie przez rozwiązanie podstawowego równania mechaniki kwantowej – równania Schrödingera. Równanie falowe Schrödingera jest w sposób istotny powiązane z teorią de Broglie’a, która daje opis falowy ruchu cząstek. Obecnie pokażemy jak pierwszy postulat Bohra wynika w sposób prosty z hipotezy de Broglie’a.

Zgodnie z hipotezą de Broglie’a elektronowi o pędzie mv przypisujemy falę o długości

(2.96)

a więc zamiast mówić o ruchu elektronu wewnątrz atomu po stałej orbicie, można rozpatrywać ruch ciągu fal de Broglie’a związanych z elektronem poruszającym się po tej orbicie. Gdyby na orbicie kołowej mieściła się ułamkowa liczba długości fal, fale te osłabiałyby się i wygasały w bardzo krótkim czasie wskutek interferencji (Rys. 2.11) .

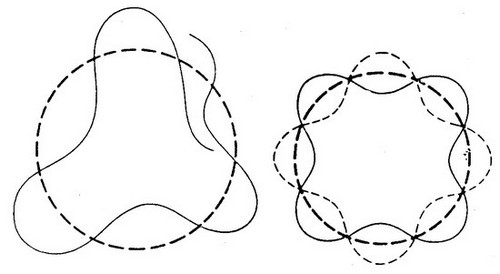(Rys. 2.11)

Aby zaś fale te nie znosiły się przez interferencję, muszą one tworzyć na orbicie stacjonarne fale stojące. Jak wiemy fala stojąca powstaje wtedy, gdy długość drogi jest całkowitą wielokrotnością długości fali, czyli gdy

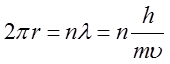(2.97)

stąd zaś wynika warunek kwantowania Bohra

(2.98)

Elektron krąży wokół jądra przez czas nieograniczenie długi nie promieniując przy tym energii na zewnątrz pod warunkiem, że jego orbita zawiera całkowitą liczbę długości fal de Broglie’a związanych z elektronem. Powyższy postulat łączy w sobie własności falowe i korpuskularne elektronu, ponieważ długość fali elektronu oblicza się z prędkości elektronu na orbicie. Związana z tą prędkością siła odśrodkowa równoważy siłę przyciągania elektrostatycznego jądra. Potwierdza to jeszcze raz fakt, że obie natury elektronu: korpuskularna i falowa, mimo że nie możemy ich badać równocześnie, są nierozłączne w przyrodzie.

2.10 Wzbudzanie atomów

Atomy wzbudzone do wyższych poziomów energetycznych tracą energię wzbudzenia przez wypromieniowanie. Atom może być wzbudzony w dwojaki sposób:

1) przez zderzenie z cząstką o dużej energii kinetycznej; atom może wówczas przejąć część energii tej cząstki,

2) przez absorpcję kwantów promieniowania.

Pierwszy rodzaj wzbudzenia zachodzi podczas wyładowania elektrycznego w gazach rozrzedzonych. Pole elektrostatyczne które przyspiesza znajdujące się w gazie jony i elektrony, musi być tak silne, aby energia uzyskana przez te cząstki między zderzeniami była dostatecznie duża na dokonanie wzbudzenia.

Wzbudzenie atomu przez absorpcję kwantu promieniowania zachodzi wówczas, gdy energia kwantu wynosi dokładnie tyle ile potrzeba aby podnieść energię atomu na wyższy dozwolony poziom energetyczny.

Proces ten tłumaczy powstawanie widm absorpcyjnych. Ze światła białego po przejściu np. przez warstwę wodoru znajdującego się w naczyniu o ścianach przezroczystych zostają zaabsorbowane te fotony, których energie odpowiadają przejściom elektronów między poziomami energetycznymi atomu wodoru. Wzbudzone atomy wodoru emitują natychmiast po wzbudzeniu pochłoniętą energię, wysyłając fotony w kierunkach zupełnie przypadkowych, tak że tylko część z nich biegnie w kierunku pierwotnej wiązki światła białego. To powoduje, że linie w widmie absorpcyjnym nigdy nie są całkowicie czarne, jedynie tak wyglądają wskutek kontrastu z kolorowym tłem. Doświadczenie potwierdza, jak należało oczekiwać, że widmo absorpcyjne dowolnego pierwiastka jest identyczne pod względem reprezentowanych długości fal z widmem emisyjnym tegoż pierwiastka.

2.11 Doświadczenie Francka-Hertza

Oprócz badania widma atomowego danego pierwiastka znane są też inne metody pozwalające wnioskowac o poziomach energetycznych atomu. W roku 1914 Franck i Hertz przeprowadzili doświadczenia dotyczące mechanizmu wzbudzenia atomów przez wyładowanie w polu elektrycznym i otrzymali interesujące rezultaty odnośnie poziomów energetycznych atomu. Doświadczenia te wykazały, że poziomy takie rzeczywiście istnieją i że pokrywają się one z poziomami, o których istnieniu można było wnioskować na podstawie obserwacji widm liniowych.

Schemat aparatury Francka i Hertza jest przedstawiony na rysunku 2.12

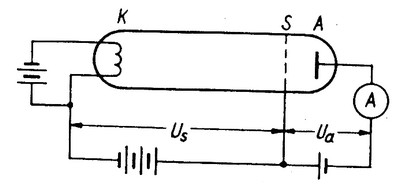(Rys. 2.12)

W naczyniu szklanym zawierającym trzy elektrody: żarzoną katodę K, siatkę S i anodę A znajduje się para rtęci. Elektrony wylatujące z rozżarzonej katody są przyspieszane napięciem U_s między katodą i siatką, i są hamowane napięciem U_a między anodą i siatką tak, że jedynie elektrony, których energia (w miejscu gdzie znajduje się siatka) jest większa od pewnej energii minimalnej U₀e zostają zebrane przez anodę i dają przyczynek do prądu mierzonego przez galwanometr. Ze wzrosem napięcia przyspieszającego U_s coraz więcej elektronów trafia do anody i prąd anodowy rośnie. Okazuje się jednak, że po osiągnięciu przez elektrony pewnej energii krytycznej prąd anodowy nagle maleje (Rys. 2.13).

(Rys. 2.13)

Fakt ten tłumaczy się następująco.

W procesie zderzenia sprężystego elektronów z atomami rtęci elektrony prawie nie tracą energii (z powodu małej masy elektronu w stosunku do masy atomu rtęci), zmieniając w zderzeniach jedynie kierunek swej prędkości. Po osiągnięciu jednak dostatecznej energii podczas zderzenia z atomem rtęci elektron przekazuje mu część albo całą swoją energię kinetyczną podnosząc energię atomu na poziom wyższy niż podstawowy. Ten rodzaj zderzenia w odróżnieniu od zderzenia sprężystego, w którym jest zachowana energia kinetyczna, nazywa się zderzeniem niesprężystym. Energia krytyczna, przy której zachodzi spadek natężenia prądu anodowego, równa się energii wzbudzenia atomu rtęci, gdyż tylko taką porcję energii może atom rtęci zaabsorbować. Dla par rtęci wynosi ona 4,86 eV.

W miarę dalszego wzrostu napięcia przyspieszającego U_s prąd anodowy znowu narasta (energia elektronów po pierwszym zderzeniu narasta i znów osiąga wartość wystarczającą aby elektrony mogły osiągnąć anodę). Gdy U_s = 2⋅4,86 V, elektron może doznać dwóch kolejnych zderzeń niesprężystych i krzywa prądu anodowego wykazuje nowe głębokie minimum. Wynika stąd, że potencjał krytyczny powodujący wzbudzenie atomu rtęci wynosi około 4,86 V. Bardziej złożone doświadczenia wykazują, że dla atomów rtęci występują również wyższe potencjały wzbudzenia, które nie są pokazane na krzywej z rysunku 2.13, ponieważ z chwilą gdy energia elektronu osiągnie wartość 4,86 eV, elektron traci ją w zderzeniu niesprężystym. Z tych względów jest rzeczą mało prawdopodobną, aby elektron uzyskał dostatecznie dużą energię dla dokonania wzbudzenia atomu do wyższych poziomów energetycznych.

W celu sprawdzenia, że występowanie potencjału krytycznego jest wynikiem istnienia określonych dyskretnych poziomów energetycznych atomu, Franck i Hertz badali widmo emisyjne pary rtęci wysyłane podczas bombardowania jej elektronami. Stwierdzili oni, że minimalna energia elektronów dla wzbudzenia linii 2536 angstremów wynosi 4,86 eV, a energia kwantów o tej długości fali wynosi właśnie hν = 4,86 eV. Dla zaobserwowania wymienionej linii parę rtęci należy umieścić w naczyniu kwarcowym, ponieważ szkło jest dla tej długości fali materiałem nieprzezroczystym.

2.12 Zasada odpowiedniości

Zgodnie z wprowadzoną przez Bohra zasadą odpowiedniości dla dużych liczb kwantowych i dla małych ich różnic mechanika kwantowa i fizyka klasyczna dają te same rezultaty.

Według teorii elektromagnetycznej elektron poruszający się po orbicie kołowej promieniuje fale elektromagnetyczne o częstotliwości równej częstotliwości jego ruchu po orbicie i o wyższych harmonicznych tej częstotliwości. Dla atomu wodoru prędkość po orbicie wynosi

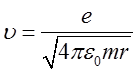(2.99)

co wynika z przyrównania siły dośrodkowej do siły kulombowskiej, stąd częstotliwość ruchu po orbicie kołowej wynosi

(2.100)

Promień stacjonarnej orbity kołowej, dla której liczba kwantowa wynosi n, równa się

(2.101)

i stąd częstotliwość obiegu

(2.102)

W myśl zasady odpowiedniości dla orbit elektronu tak dużych, że można by było je bezpośrednio mierzyć, należy oczekiwać, że efekty kwantowe będą bardzo małe i przewidywania kwantowej teorii Bohra będą pokrywać się z przewidywaniami teorii klasycznej. Przyjmijmy zatem, że średnica bardzo odległej orbity elektronu w atomie wodoru wynosi 1 cm, co w przybliżeniu odpowiada liczbie kwantowej n = 10 000. Oczywiście atom wodoru o tak dużych rozmiarach nie istnieje, ponieważ poziom energetyczny takiego atomu różniłby się nieskończenie mało od atomu wodoru w stanie zjonizowanym. Jednak taki atom nie jest zabroniony przez teorię Bohra. Zgodnie z teorią Bohra atom wodoru przechodząc ze stanu określonego liczbą kwantową n do stanu określonego liczbą kwantową n – p emituje foton o częstotliwości

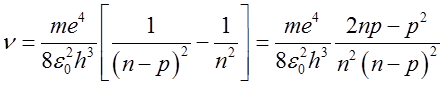(2.103)

Dla dużych wartości n i małych wartości p mamy

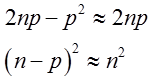(2.104)

wobec czego

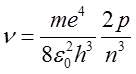(2.105)

Dla wartości p = 1 wzór (2.105) pokrywa się dokładnie ze wzorem (2.102) na częstotliwośc klasyczną f. Dla wartości p = 2, 3, 4, atom emituje wyższe harmoniczne częstotliwości podstawowej f. A więc zarówno model klasyczny jak i kwantowy atomu wodoru w granicznym przypadku dużych liczb kwantowych dają jednakowe rezultaty.